NCERT Solutions for Class 9 Maths Chapter 12 PDF covers the topic of triangles, different types of triangles and the formulas to calculate the areas of triangle. The chapter also discusses Herons formula and area of trapezoid
Area of Triangle:
A triangle is a regular polygonal structure which has three sides. The sum of all angles is 180 degrees.
Area of a right- angled triangle:
A triangle in which one of the angles is right angle, then it is a right angled triangle. The sum of two sides of a triangle is greater than the third side.
Area of an equilateral triangle:
An equilateral triangle is a triangle whose all sides are equal. The formula can be found with the following formulas
where s is the length of the side of the triangle.
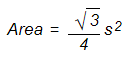
Area of a trapezium:
The area of triangle can be provided with two formulas
- The area of trapezium can be defined as product of half the sum of parallel sides and the perpendicular distance between the two.
= 1/2 (sum of parallel sides) × (perpendicular distance between them)
- The area of a typical trapezium can be given as sum of area of two triangles as given below
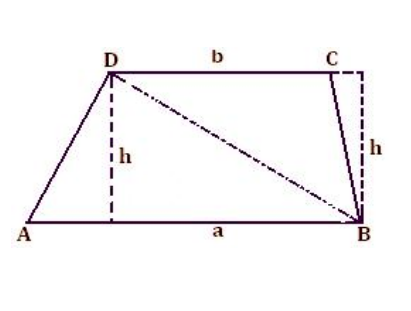
Area of trapezium ABCD = Area of ∆ ABD + Area of ∆ CBD
= 1/2 × a × h + 1/2 × b × h
= 1/2 × h × (a + b)
Heron’s Formula:
The formula was developed by Hero of Alexandria, so it called as Hero’s formula or Heron’s formula. It helps in providing the area of the triangle. Basically, area of a triangle is found based on side or vertex.
As per Heron’s formula, the area of a triangle can be represented as
Where a, b, and c represents the sides of the triangle
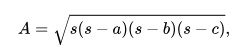
s is the semiperimeter of the triangle; which can be calculated by the formula
![]()
Heron’s formula can also be rewritten as
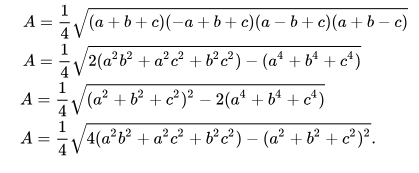
Herons formula class 9 is an important question in Class 9 NCERT solutions











