Exercise 11.1

1) Draw a line segment of length 7.6 cm and divide it in 5: 8 ration. In addition, find the measure of two parts.

Solution:

Procedure for construction:

1. Draw any ray AX, making an acute angle with AB.
2. Locate 13(= 5 + 8) points A₁, A₂, A₃ ……… A13 on AX so that AA₁ = A₁A₂ A_l2 A₁₃.
3. Join BA₁₃.
4. Through the point A5(m = 5), draw a line parallel to BA13 (by making an angle equal to L AA13 B at A5 intersecting AB at C. Then AC: CB = 5 : 8)

2) Construct a triangle with sides 4 cm, 5 cm and 6 cm and then a similar triangle to it whose sides are 2/3 of the corresponding sides of the first one.

Solution:

Procedure for construction:

1. Draw a line segment BC with length 5 cm.
2. With B as centre and radius of 4 cm draw an arc.
3. With C as centre and radius of 6 cm draw an arc.
4. Join AB and AC. Then, ∆ABC is the required triangle.
5. Below BC, make an acute angle ∠CBX
6. Along BX, mark up three points B1, B2, B3 such that BB1 = B₁ B₂ = B₂B₃
7. Join B₃C
8. From B2, draw B₂C’llB₃c, meeting BC at C’
9. From C’ draw C’ All CA, meeting BA at A’
10. Then ∆A’BC’ is the required triangle, each of whose sides is two-third of the corresponding sides of ∆ABC.

3) Construct a triangle with side lengths 5 cm, 6 cm and 7 cm and then another triangle whose sides are  of the corresponding sides of the first triangle.

Solution:

Procedure for  construction :

1. Draw a line segment BC with length 6 cm.
2. With B as centre and keeping radius as 5 cm, draw an arc.
3. With C as centre and keeping radius as 7 cm, draw another arc, intersecting the previously drawn arc at Point A.
4. Join AB and AC. Then, ∆ABC is the required triangle.
5. Below BC, make an acute angle∠CBX.
6. Along BX, mark up seven points B₁, B₂, B₃….. B₇ such that BB₁ = B₁,B₂, B₆B₇.
7. Join B₅ to C (5 being smaller of 5 and 7 in7/5) and draw a line through B₇ parallel to B₅C, intersecting the extended line segment BC at C’.
8. Draw a line through C’ parallel to CA intersecting the extended line segment BA at A’. Then A’BC’ is the required triangle.

4) Draw a triangle ABC with sides BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are ¾ of the corresponding sides of ∆ABC.

Solution:

Procedure for construction:

(i)            Draw a triangle ABC with BC = 6 cm, AB = 5 cm and ∠ABC = 60°.

(ii)           Draw any ray BX making an acute angle with BC on the side opposite to the vertex X.

(iii)          Locate 4(the greater of 3 and 4 in ¾) points B1, B2, B3, B4 on BX so that BB₁ = B₁B₂ = B₂B₃ = B₃B₄.

(iv)         Join B₄C and draw a line through B3(the 3rd point, 3 being smaller of 3 and 4 in ¾) parallel to B₄C to intersect BC at C’.

(v)          Draw a line through C’ parallel to the line CA to intersect BA at A’. Then ∆A’BC’ is the required triangle.

Justification of construction

∆ABC ~ ∆A’BC’ , Therefore,

ABA′B=ACA′C′=BCBC′

But, BCBC′=BB3BB4=34

So, ABA′B=ACA′C′=BCBC′=34
5) Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are4/3 times the corresponding sides of ∆ABC.

Solution:

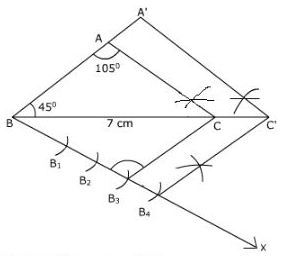
Procedure for  construction :

(i)            Draw a triangle ABC with BC = 7cm, ∠B = 45° and ∠A = 105°.

(ii)           Draw any ray BX making an acute angle with BC on the side opposite to the vertex X.

(iii)          Locate 4(the greater of 3 and 4 in 4/3) points B₁, B₂, B₃, B₄ on BX so that 3 BB₁ = B₁ B₂ = B₂B₃ = B₃B₄.

(iv)         Join NC’ and draw a line through B3(the 3rd point, 3 being smaller of 3 and 4 in 1) parallel to NC’ to intersect BC’ at C. 3

(v)          Draw a line through C’ parallel to the line CA to intersect BA at A’. Then A NBC’ is the required triangle.

6) Construct a triangle of isosceles type, whose base is 8 cm and height 4 cm and then another triangle whose sides are 1.5 times the corresponding sides of the isosceles triangle.

Solution:

Given:An isosceles triangle whose base is 8 cm and height 4 cm. Scale factor: 1  =

Required: To construct a similar triangle to above whose sides are 1.5 times the above triangle.

Procedure for construction:

(i)            Draw a line segment BC = 8 cm.

(ii)           Draw a perpendicular bisector AD of BC.

(iii)          Join AB and AC we get a isosceles ∆ABC.

(iv)         Construct an acute angle∠CBX downwards.

(v)          On BX make 3 equal parts.

(vi)         Join C to B₂ and draw a line through B₃ parallel to B₂C intersecting the extended line segment BC at C’.

(vii)        Again draw a parallel line C’A’ to AC cutting BP at A’.

(viii)       ∆A’BC’ is the required triangle.

Exercise 11.2

7) Draw a circle with radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.

Solution:

Procedure for construction:

1. Draw a line segment of length AB = 10 cm. Bisect AB by constructing a perpendicular bisector of AB. Let M be the mid-point of AB.
2. With M as centre and AM as radius, draw a circle. Let it intersect the given circle at the points P and Q.
3. Join PB and QB. Thus, PB and QB are the required two tangents.

Justification: Join AP. Here ∠APB is an angle in the semi-circle. Therefore, ∠APB = 90°. Since AP is a radius of a circle, PB has to be a tangent to a circle. Similarly, QB is also a tangent to a circle.

In a Right ∆APB, AB² = AP² + PB² (By using Pythagoras Theorem)
PB² = AB² – AP² = 10² — 6² = 100 – 36 = 64

PB = 8 cm.

8) Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.

Solution:

Procedure for construction:

1. Draw a line segment of length OA = 4 cm. With O as centre and OA as radius, draw a circle.
2. With O as centre draw a concentric circle of radius 6 cm(0B).
3. Let C be any point on the circle of radius 6 cm, join OC.
4. Bisect OC such that M is the mid point of OC.
5. With M as centre and OM as radius, draw a circle. Let it intersect the given circle of radius 4 cm at the points P and Q.
6. Join CP and CQ. Thus, CP and CQ are the required two tangents.

Justification:

Join OP. Here ∠OPC is an angle in the semi-circle. Therefore, ∠OPC = 90°. Since OP is a radius of a circle, CP has to be a tangent to a circle. Similarly, CQ is also a tangent to a circle.

In ∆COP, ∠P = 90°

CO2=CP2+OP2 CP2=CO2–OP2

=62–42

CP=25–√cm

9) Draw a circle with radius 3 cm. On one of its extended diameter, take two points P and Q each at a distance of 7 cm from its centre. From two points P and Q, draw tangents to the circle.

Solution:

Given:

Two points P and Q on the diameter of a circle with radius 3 cm OP = OQ = 7 cm.

Aim:

To construct the tangents to the circle from the given points P and Q.

Procedure for construction:

1. Draw a circle with radius 3 cm with centreO.
2. Extend its diameter both the sides and cut OP = OQ = 7 cm.
3. Bisect OP and OQ.Let mid-points of OP and OQ be M and N.
4. With M as centre and OM as radius, draw a circle. Let it intersect (0, 3) at two points A and B. Again taking N as centre ON as radius draw a circle to intersect circle(0, 3) at points C and D.
5. Join PA, PB, QC and QD. These are the required tangents from P and Q to circle (0, 3).

10) Draw a pair of tangents to a circle which is of radius 5 cm, such that they are inclined to each other at an angle of 60°.

Solution:

To determine: To draw tangents at the ends of two radius which are inclined to each other at 120°

Procedure for  construction :

1. Keeping O as centre, draw a circle of radius 5 cm.
2. Take a point Q on the circle and join it to O.
3. From OQ, Draw∠QOR = 120°.
4. Take an external point P.
5. Join PR and PQ perpendicular to OR and OQ respectively intersecting at P.

The required tangents are RP and QP.

Related Links