Download Trigonometry Formulas PDF
Introduction:
The word Trigonometry is derived from the Greek word trigōnon means “triangle” and metron means “measure. It is a branch of mathematics which deals with the relationship between lengths, height and angles of triangle. The subject was introduced in 3rd century BC while applying geometry formulas to the astronomical studies. Trigonometry finds applications in number of fields such as
- Engineering
- Astronomy
- Physics and
- Architectural design
Trigonometry formulas are for class 10 has important topics of Linear Algebra, Calculus and Statistics. Inorder to master over the topics, the students are required to understand and learn all the formulas and correctly apply the formulas to solve the subjects.
Click here to Download Trigonometry Formulas
Trigonometric Ratios:
It provides the relationship between the angles and length of the side (adjacent, opposite and hypotenuse) of the right angle triangle.
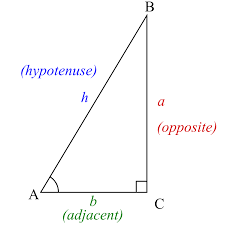
The Sides:
The different sides of the triangle are referred to as opposite, adjacent, and hypotenuse as shown in the figure
Adjacent side is always next to the angle
Opposite as the name says it is opposite to the angle
Inorder to learn trigonometric ratios, students should understand the following terms of a rectangle
Sinθ= length of opposite side/ length of hypotenuse
Cosθ= length of adjacent side/ length of hypotenuse
Tanθ= length of opposite side/ length of adjacent side
cscθ = length of hypotenuse/ length of opposite side
secθ= length of hypotenuse side/ length of adjacent side
cotθ = length of adjacent side/ length of opposite side
Trigonometric Identities:
Trigonometric Identities refer to all types of angles not just right angle triangle.
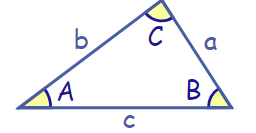
Law of Sines
![]()
It can also be re-arranged to:
![]()
Law of Cosines
![]()
It can also be re-arranged to:
![]()
Law of Tangents
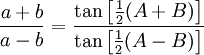
Trigonometric Ratios of Complementary Angles:
Any two angles whose sum is equal to 90°
Thus, two angles X and Y are complementary if,
∠X + ∠Y = 90°
∠X is known as the complement of ∠Y and vice-versa.
Ina right angled triangle, the remaining two angles are always complementary.
Make list of Trigonometry formulas or you can also make Trigonometry formulas pdf and store in the mobile or in the desktop to learn.